聰明不如鈍筆
총명불여둔필


오랜만에 페이스북에 들어갔다가 'R Korea - KRSG(Korean R Study Group)'에 올라온 이 글을 보게 됐습니다.
R로 분산분석(ANOVA·Analysis of Variance)을 진행하는 내용입니다.
ANOVA는 그룹이 세 개 이상일 때 평균 차이가 통계적으로 유의미하다고 할 수 있는지 아닌지 알아보는 작업입니다.
먼저 어떤 글이 올라왔는지 한 번 읽어보겠습니다.
안녕하세요? 과제를 하다가 막히는 부분이 있어서 글 올립니다. ^^ 일원분산분석하는 문제인데요. 코드는 아래와 같습니다.
=================================
개복수술 <- c(12, 10, 14, 12, 11, 9, 9, 11, 11, 😎
복강경수술 <- c(9, 7, 8, 6, 6, 7, 10, 10)
로봇수술 <- c(5, 6, 7, 7, 7, 4, 5)
boxplot(개복수술, 복강경수술, 로봇수술, main = "직장암 환자들의 각 수술 방법 별 입원기간", names=c("개복수술", "복강경수술", "로봇수술") , ylab = "입원일수")
points(c(mean(개복수술), mean(복강경수술), mean(로봇수술)), pch=10 , cex=2)
입원일수 = c(개복수술, 복강경수술, 로봇수술)
그룹 = factor(rep(c("개복수술", "복강경수술", "로봇수술"), c(10, 8, 7)))
일원분산분석 = aov(입원일수 ~ 그룹)
일원분산분석
summary(일원분산분석)
=================================
summary(일원분산분석) 은 제대로 표시가 됩니다. p값도 제대로 나옵니다. 문제는 "일원분산분석 " 이 제대로 표시가 안 됩니다. 원래 call:
aov
이렇게 내용이 나와 줘야 하는데 첨부한 사진대로 출력이 됩니다. 왜 그런가요? 고수분들의 도움이 필요합니다. 감사합니다. ^^

kini註 - 선글라스 이모티콘은 제가 넣은 게 아니라 원래 게시물에 그렇게 올라왔습니다.
tidyverse 사투리를 사랑하는 제 눈에는 이 코드가 어딘지 어수선하게 보입니다.
그게 꼭 중간에 상자-수염 그래프를 그리는 코드가 들어가 있기 때문만은 아닙니다.
ANOVA를 진행하기 전 데이터를 정리하는 과정부터 복잡합니다.
똑같은 작업을 하는 코드를 tidyverse 스타일로 쓰면 이렇게 정리할 수 있습니다.
enframe(
list(개복 = c(12, 10, 14, 12, 11, 9, 9, 11, 11),
복강경 = c(9, 7, 8, 6, 6, 7, 10, 10),
로봇 = c(5, 6, 7, 7, 7, 4, 5))
) %>%
unnest(value) %>%
mutate(name = name %>% as_factor()) %>%
aov(value ~ name, data = .)
물론 tidyverse 스타일에 익숙하지 않은 분께는 이쪽이 더 난해하게 보일 수도 있습니다.
그래도 일단 '보기에는' 더 깔끔하다고 생각하지 않으십니까?
이번 포스트에서는 tidyverse, tidymodels 패키지를 활용해 ANOVA를 진행하는 방법을 알아보도록 하겠습니다.
아, 그 전에 먼저 게시자께서는 올리신 코드를 돌려 보겠습니다.
게시자께서는 코드가 작동하지 않는다고 하셨는데 실제로는 잘 돌아갑니다.
개복수술 <- c(12, 10, 14, 12, 11, 9, 9, 11, 11)복강경수술 <- c(9, 7, 8, 6, 6, 7, 10, 10)로봇수술 <- c(5, 6, 7, 7, 7, 4, 5)boxplot(개복수술, 복강경수술, 로봇수술, main = "직장암 환자들의 각 수술 방법 별 입원기간",
names=c("개복수술", "복강경수술", "로봇수술"), ylab = "입원일수")points(c(mean(개복수술), mean(복강경수술), mean(로봇수술)), pch=10 , cex=2)
입원일수 = c(개복수술, 복강경수술, 로봇수술)입원일수## [1] 12 10 14 12 11 9 9 11 11 9 7 8 6 6 7 10 10 5 6 7 7 7 4 5
그룹 = factor(rep(c("개복수술", "복강경수술", "로봇수술"), c(9, 8, 7)))그룹## [1] 개복수술 개복수술 개복수술 개복수술 개복수술 개복수술 ## [7] 개복수술 개복수술 개복수술 복강경수술 복강경수술 복강경수술 ## [13] 복강경수술 복강경수술 복강경수술 복강경수술 복강경수술 로봇수술 ## [19] 로봇수술 로봇수술 로봇수술 로봇수술 로봇수술 로봇수술 ## Levels: 개복수술 로봇수술 복강경수술
일원분산분석 = aov(입원일수 ~ 그룹)일원분산분석## Call: ## aov(formula = 입원일수 ~ 그룹) ## ## Terms: ## 그룹 Residuals ## Sum of Squares 108.22619 47.73214 ## Deg. of Freedom 2 21 ## ## Residual standard error: 1.507634 ## Estimated effects may be unbalanced
summary(일원분산분석)## Df Sum Sq Mean Sq F value Pr(>F) ## 그룹 2 108.23 54.11 23.81 3.99e-06 *** ## Residuals 21 47.73 2.27 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
요컨대 R로 ANOVA를 진행할 때는 사실 aov() 함수 하나만 알고 있으면 됩니다.
또 summary() 함수 출력 결과 그룹에 별(*)에 세 개 떴으니까 유의확률(p-값)이 0.001보다 작다는 사실을 알 수 있습니다.
p-값이 특정한 문턱값보다 작다고 곧바로 통계적으로 유의미하다고 결론을 내리는 건 성급한 결정입니다.
다만 이 값이 0.05 이하일 때는 이 값이 통계적으로 유의미하다고 보는 게 관례입니다.
(0.05 = 5%를 기준으로 삼았다는 것부터 특정한 이유가 있다기보다 그저 '관례'라는 증거가 됩니다.)

그러면 이제부터 이 코드를 tidyverse 스타일로 바꾸는 과정을 차근차근 살펴 보도록 하겠습니다.
일단 먼저 tidyverse 패키지를 (설치하고) 불러옵니다.
#install.packages('tidyverse')
library('tidyverse')## -- Attaching packages --------------------------------------- tidyverse 1.3.1 --
## v ggplot2 3.3.5 v purrr 0.3.4 ## v tibble 3.1.4 v dplyr 1.0.7 ## v tidyr 1.1.3 v stringr 1.4.0 ## v readr 2.0.1 v forcats 0.5.1
## -- Conflicts ------------------------------------------ tidyverse_conflicts() -- ## x dplyr::filter() masks stats::filter() ## x dplyr::lag() masks stats::lag()
만약 이 패키지를 불러오지 않으셨다면 위에서 소개해 드린 tidyverse 스타일 코드가 작동하지 않았을 겁니다.
이제 패키지를 준비했으니 데이터를 입력합니다.
게시자께서는 입원일수와 그룹을 따로따로 두고 ANOVA를 진행하셨는데 굳이 그럴 필요없습니다.
이미 게시자께서 데이터를 입력해 놓은 게 있으니까 enframe()과 list() 함수를 써서 데이터 프레임 조금 더 정확하게는 tibble로 만들어 보겠습니다.
enframe()은 벡터 그러니까 c() 함수로 묶은 데이터를 tibble로 만드는 구실을 하는 함수입니다.
enframe(
list(개복 = c(12, 10, 14, 12, 11, 9, 9, 11, 11),
복강경 = c(9, 7, 8, 6, 6, 7, 10, 10),
로봇 = c(5, 6, 7, 7, 7, 4, 5))
) ## # A tibble: 3 x 2 ## name value ## <chr> <list> ## 1 개복 <dbl [9]> ## 2 복강경 <dbl [8]> ## 3 로봇 <dbl [7]>
이런 형태가 익숙하지 않은 분이 적지 않으실 겁니다. 이 tibble은 value 열에 리스트가 들어 있는 상태입니다.
이런 형태를 중첩(nested) tibble이라고 부릅니다. unnest() 함수를 쓰면 중첩 상태를 해제할 수 있습니다.
우리가 열어서 확인하고 싶은 데이터는 value 열에 있으니까 unnest(value)라고 씁니다.
enframe(
list(개복 = c(12, 10, 14, 12, 11, 9, 9, 11, 11),
복강경 = c(9, 7, 8, 6, 6, 7, 10, 10),
로봇 = c(5, 6, 7, 7, 7, 4, 5))
) %>%
unnest(value)## # A tibble: 24 x 2 ## name value ## <chr> <dbl> ## 1 개복 12 ## 2 개복 10 ## 3 개복 14 ## 4 개복 12 ## 5 개복 11 ## 6 개복 9 ## 7 개복 9 ## 8 개복 11 ## 9 개복 11 ## 10 복강경 9 ## # ... with 14 more rows
이렇게 우리는 그룹별 데이터 개수를 일일이 세어야 하는 rep() 함수를 쓰지 않고도 똑같은 데이터를 확보했습니다.
이런 식으로 자료를 정리하면 데이터가 새로 들어와도 그냥 c() 함수 안에 넣기만 하면 됩니다.
원래 코드에서는 데이터가 늘어나면 rep() 함수 안에 있는 숫자를 일일이 조절해야 했습니다.
또 이번에는 게시자께서 데이터를 벡터로 제공하셔서 이런 식으로 처리했지만 어떤 자료든지 일단 tibble로 만들기만 하면 나머지 과정은 똑같습니다.
예를 들어 아래 있는 파일을 내려받으신 다음 read.csv() 같은 함수로 불러오셔도 똑같이 작동합니다.
아, 혹시 '%>%' 이렇게 생긴 파이프 기호가 무슨 뜻인지 모르시는 분은 '최대한 친절하게 쓴 R로 데이터 뽑아내기(feat. dplyr)' 포스트가 도움이 될 수 있습니다.
현실 세계에서 파이프가 액체나 기체가 이동할 수 있는 통로 구실을 하는 것처럼 tidyverse에서 파이프 역시 데이터를 이 함수에서 저 함수로 옮겨줍니다.
위에서는 enframe(list(...)) 결과를 unnest() 함수로 옮겨준 겁니다.

R에서 ANOVA를 진행할 때는 그룹 이름을 팩터(factor)로 바꿔줘야 합니다. 말 자체는 어려울 수 있지만 사실 별 거 아닙니다.
어떤 서비스에 대해 '마음에 들지 않음', '보통', '마음에 듦' 같은 형태로 설문조사한 데이터가 바로 팩터형입니다.
이 자료가 보통 텍스트라면 '마음에 들지 않음', '마음에 듦', '보통' 순서로 오름차순 정렬을 하는 게 맞지만 그렇게 하면 이상하다는 걸 직관적으로 느낄 수 있습니다.
이렇게 데이터를 어떤 카테고리에 따라 나누는 형태가 바로 팩터형입니다.

어떤 자료를 팩터형으로 바꾸고 싶을 때는 as_factor() 함수만 적용하면 됩니다.
우리는 name 열을 팩터형으로 바꾸고 싶으니까 'name %>% as_factor()'라고 쓰면 그만입니다.
이를 다시 원래 name 열 자리에 넣어줍니다.
그러려면 mutate() 함수를 써서 'mutate(name = name %>% as_factor()'라고 쓰면 됩니다.
이 부분이 이해가 가지 않으시는 분도 '최대한 친절하게 쓴 R로 데이터 뽑아내기(feat. dplyr)' 포스트를 참고하시면 좋습니다.
enframe(
list(개복 = c(12, 10, 14, 12, 11, 9, 9, 11, 11),
복강경 = c(9, 7, 8, 6, 6, 7, 10, 10),
로봇 = c(5, 6, 7, 7, 7, 4, 5))
) %>%
unnest(value) %>%
mutate(name = name %>% as_factor())## # A tibble: 24 x 2 ## name value ## <fct> <dbl> ## 1 개복 12 ## 2 개복 10 ## 3 개복 14 ## 4 개복 12 ## 5 개복 11 ## 6 개복 9 ## 7 개복 9 ## 8 개복 11 ## 9 개복 11 ## 10 복강경 9 ## # ... with 14 more rows
이렇게 코드를 입력한 다음 확인해 보면 name 열이 팩터형(<fct>)으로 바뀐 걸 알 수 있습니다.
이제 aov() 함수를 써서 ANOVA를 진행하면 그만입니다.
우리가 알아보고자 하는 건 수술 방식(name)에 따라 평균 입원일수(value)가 달라지느냐 하는 것. 이는 aov(value ~ name) 형태로 쓰면 됩니다.
이 열은 지금까지 우리가 다룬 데이터 안에 들어 있습니다. tidyverse 생태계에서 바로 위에 있는 데이터를 나타내는 기호는 '.'(마침표)입니다.
따라서 aov(value ~ name, data = .)라고 쓰시면 ANOVA를 진행할 수 있습니다.
enframe(
list(개복 = c(12, 10, 14, 12, 11, 9, 9, 11, 11),
복강경 = c(9, 7, 8, 6, 6, 7, 10, 10),
로봇 = c(5, 6, 7, 7, 7, 4, 5))
) %>%
unnest(value) %>%
mutate(name = name %>% as_factor()) %>%
aov(value ~ name, data = .)## Call: ## aov(formula = value ~ name, data = .) ## ## Terms: ## name Residuals ## Sum of Squares 108.22619 47.73214 ## Deg. of Freedom 2 21 ## ## Residual standard error: 1.507634 ## Estimated effects may be unbalanced
물론 이 뒤에 곧바로 summary() 함수도 적용할 수 있습니다.
enframe(
list(개복 = c(12, 10, 14, 12, 11, 9, 9, 11, 11),
복강경 = c(9, 7, 8, 6, 6, 7, 10, 10),
로봇 = c(5, 6, 7, 7, 7, 4, 5))
) %>%
unnest(value) %>%
mutate(name = name %>% as_factor()) %>%
aov(value ~ name, data = .) %>%
summary()## Df Sum Sq Mean Sq F value Pr(>F) ## name 2 108.23 54.11 23.81 3.99e-06 *** ## Residuals 21 47.73 2.27 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
이제 여기서 한 걸음 더 나아가 보겠습니다.
앞서 말씀드렸던 것처럼 tidymodels 패키지를 활용하면 분석 결과도 (조금 더) 깔끔하게 정리할 수 있습니다.
제일 먼저 할 일은 물론 tidymodels 패키지 (설치하고) 불러오기.
#install.packages('tidymodels')
library('tidymodels')## Registered S3 method overwritten by 'tune': ## method from ## required_pkgs.model_spec parsnip
## -- Attaching packages -------------------------------------- tidymodels 0.1.3 --
## v broom 0.7.9 v rsample 0.1.0 ## v dials 0.0.10 v tune 0.1.6 ## v infer 1.0.0 v workflows 0.2.3 ## v modeldata 0.1.1 v workflowsets 0.1.0 ## v parsnip 0.1.7 v yardstick 0.0.8 ## v recipes 0.1.17
## -- Conflicts ----------------------------------------- tidymodels_conflicts() -- ## x scales::discard() masks purrr::discard() ## x dplyr::filter() masks stats::filter() ## x recipes::fixed() masks stringr::fixed() ## x dplyr::lag() masks stats::lag() ## x yardstick::spec() masks readr::spec() ## x recipes::step() masks stats::step() ## * Use tidymodels_prefer() to resolve common conflicts.
통계 모형을 깔끔하게 정리하는 데 도움을 주는 함수 가운데 제일 먼저 알아야 할 건 tidy() 그리고 glance()입니다.
지금까지 정리한 코드에 이 두 함수를 한번에 적용하고 싶을 때는 summarise() 함수를 활용하시면 됩니다.
tidy() 함수를 쓰면 작업 결과를 정리해서 확인할 수 있고,
enframe(
list(개복 = c(12, 10, 14, 12, 11, 9, 9, 11, 11),
복강경 = c(9, 7, 8, 6, 6, 7, 10, 10),
로봇 = c(5, 6, 7, 7, 7, 4, 5))
) %>%
unnest(value) %>%
mutate(name = name %>% as_factor()) %>%
summarise(aov(value ~ name, data = .) %>% tidy())## # A tibble: 2 x 6 ## term df sumsq meansq statistic p.value ## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 name 2 108. 54.1 23.8 0.00000399 ## 2 Residuals 21 47.7 2.27 NA NA
glance() 함수로는 모형 성능을 확인할 수 있습니다.
enframe(
list(개복 = c(12, 10, 14, 12, 11, 9, 9, 11, 11),
복강경 = c(9, 7, 8, 6, 6, 7, 10, 10),
로봇 = c(5, 6, 7, 7, 7, 4, 5))
) %>%
unnest(value) %>%
mutate(name = name %>% as_factor()) %>%
summarise(aov(value ~ name, data = .) %>% glance())## # A tibble: 1 x 6 ## logLik AIC BIC deviance nobs r.squared ## <dbl> <dbl> <dbl> <dbl> <int> <dbl> ## 1 -42.3 92.6 97.3 47.7 24 0.694
이번 데이터처럼 간단한 분석 작업에는 이런 작업이 불필요해 보이는 것도 사실.
그래도 통계 분석을 진행한 다음 후속 작업이 필요할 때는 확실히 두 함수를 쓰는 게 도움이 됩니다.
이에 대해 조금 더 자세히 알고 싶으신 분은 'R로 깔끔하게 통계 모형 쓸어담기(feat. broom)' 포스트가 도움이 될 수 있습니다.
이제 게시자가 그리셨던 것처럼 상자-수염 그래프를 그려보겠습니다.
우리는 물론 tidyverse 생태계에서 시각화를 담당하는 ggplot2 패키지를 활용할 겁니다.
ggplot2 패키지가 낯설다고 생각하시는 분은 '최대한 친절하게 쓴 R로 그래프 그리기(feat. ggplot2)' 포스트가 도움이 될 수 있습니다.
ggplot2 패키지에서 상자(-수염) 그래프 그리기 담당은 geom_boxplot()입니다.
가장 기본적인 그래프를 그리는 코드는 이렇게 쓸 수 있습니다.
enframe(
list(개복 = c(12, 10, 14, 12, 11, 9, 9, 11, 11),
복강경 = c(9, 7, 8, 6, 6, 7, 10, 10),
로봇 = c(5, 6, 7, 7, 7, 4, 5))
) %>%
unnest(value) %>%
ggplot(aes(x = name, y = value)) +
geom_boxplot() 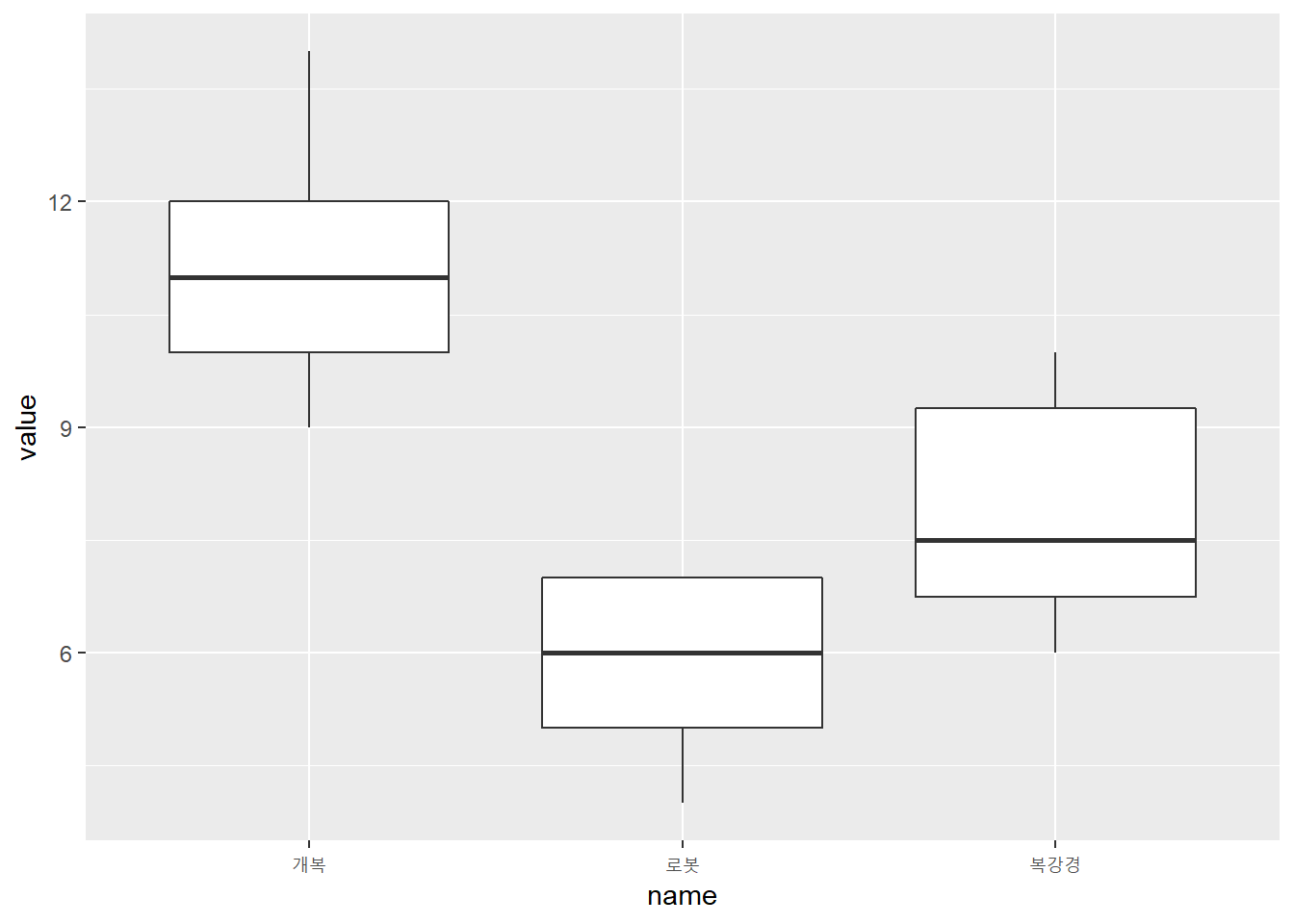
일단 가나다 순서에 따라 '개복', '로봇', '복강경'이 차례로 나타난 걸 알 수 있습니다.
value 열을 기준으로 이 순서를 조정해 주면 좋겠죠? 이럴 때 쓰는 함수는 fct_reorder()입니다.
원래 그냥 name이었던 x축 기준을 name %>% fct_reorder(value)라고 쓰면 됩니다.
enframe(
list(개복 = c(12, 10, 14, 12, 11, 9, 9, 11, 11),
복강경 = c(9, 7, 8, 6, 6, 7, 10, 10),
로봇 = c(5, 6, 7, 7, 7, 4, 5))
) %>%
unnest(value) %>%
ggplot(aes(x = name %>% fct_reorder(value), y = value)) +
geom_boxplot() 
만약 내림차순으로 바꾸고 싶을 때는 그냥 name %>% fct_reorder(-value)라고 마이너스(-) 부호만 붙이면 됩니다.
최솟값·최댓값 표시가 필요할 때는 stat_boxplot() 함수 안에 geom = 'errorbar' 옵션을 표시하면 됩니다.
이 둘을 합치면 코드를 이렇게 쓸 수 있습니다.
enframe(
list(개복 = c(12, 10, 14, 12, 11, 9, 9, 11, 11),
복강경 = c(9, 7, 8, 6, 6, 7, 10, 10),
로봇 = c(5, 6, 7, 7, 7, 4, 5))
) %>%
unnest(value) %>%
ggplot(aes(x = name %>% fct_reorder(-value), y = value)) +
stat_boxplot(geom = 'errorbar') +
geom_boxplot()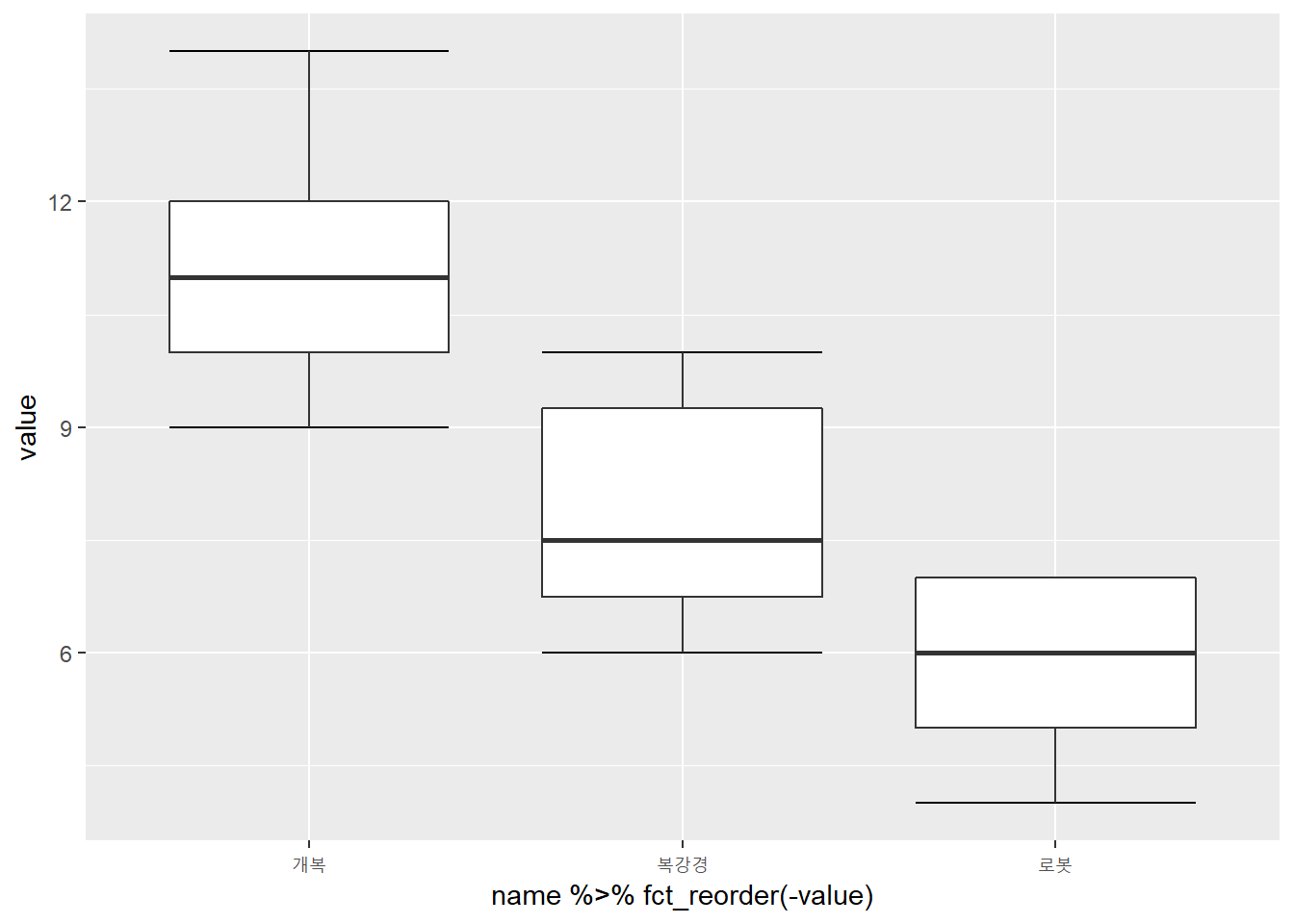
수염 길이가 너무 길다고 생각하시면 width 옵션을 통해 조절할 수 있습니다. 'width = 0.5'로 조정해 보겠습니다.
또 게시자께서 하셨던 것처럼 각 수술 방법별 평균 위치에 점도 찍어 보겠습니다.
이 때는 stat_summary()라는 함수를 활용하면 됩니다.
stat_summary() 함수 안에 평균을 구하는 mean() 함수(function)를 쓰라는 뜻에서 먼저 fun = 'mean'이라고 옵셥을 줍니다.
geom_point() 함수로 점을 찍으라는 뜻으로 geom = 'point' 옵션을 줍니다. 크기(size)는 4로 하겠습니다.
enframe(
list(개복 = c(12, 10, 14, 12, 11, 9, 9, 11, 11),
복강경 = c(9, 7, 8, 6, 6, 7, 10, 10),
로봇 = c(5, 6, 7, 7, 7, 4, 5))
) %>%
unnest(value) %>%
ggplot(aes(x = name %>% fct_reorder(-value), y = value)) +
stat_boxplot(geom = 'errorbar', width = .5) +
geom_boxplot() +
stat_summary(fun = mean, geom = 'point', size = 4)
마지막으로 labs() 함수로 제목을 달아줍니다.
그래프 전체 제목은 title, x축 제목은 x, y축 제목은 y 인수에 각각 넣어주면 됩니다.
x축 제목은 따로 필요가 없으니까 x = ''라고 입력하면 됩니다.
enframe(
list(개복 = c(12, 10, 14, 12, 11, 9, 9, 11, 11),
복강경 = c(9, 7, 8, 6, 6, 7, 10, 10),
로봇 = c(5, 6, 7, 7, 7, 4, 5))
) %>%
unnest(value) %>%
ggplot(aes(x = name %>% fct_reorder(-value), y = value)) +
stat_boxplot(geom = 'errorbar', width = .5) +
geom_boxplot() +
stat_summary(fun = mean, geom = 'point', size = 4) +
labs(title = '직장암 환자들의 각 수술 방법별 입원기간', x = '', y = '입원일수')
글씨를 쓰는 geom_text() 함수와 그래프 모양을 바꾸도록 도와주는 theme() 함수를 활용하면 이 그래프를 아래 같은 형태로 바꿀 수 있습니다.
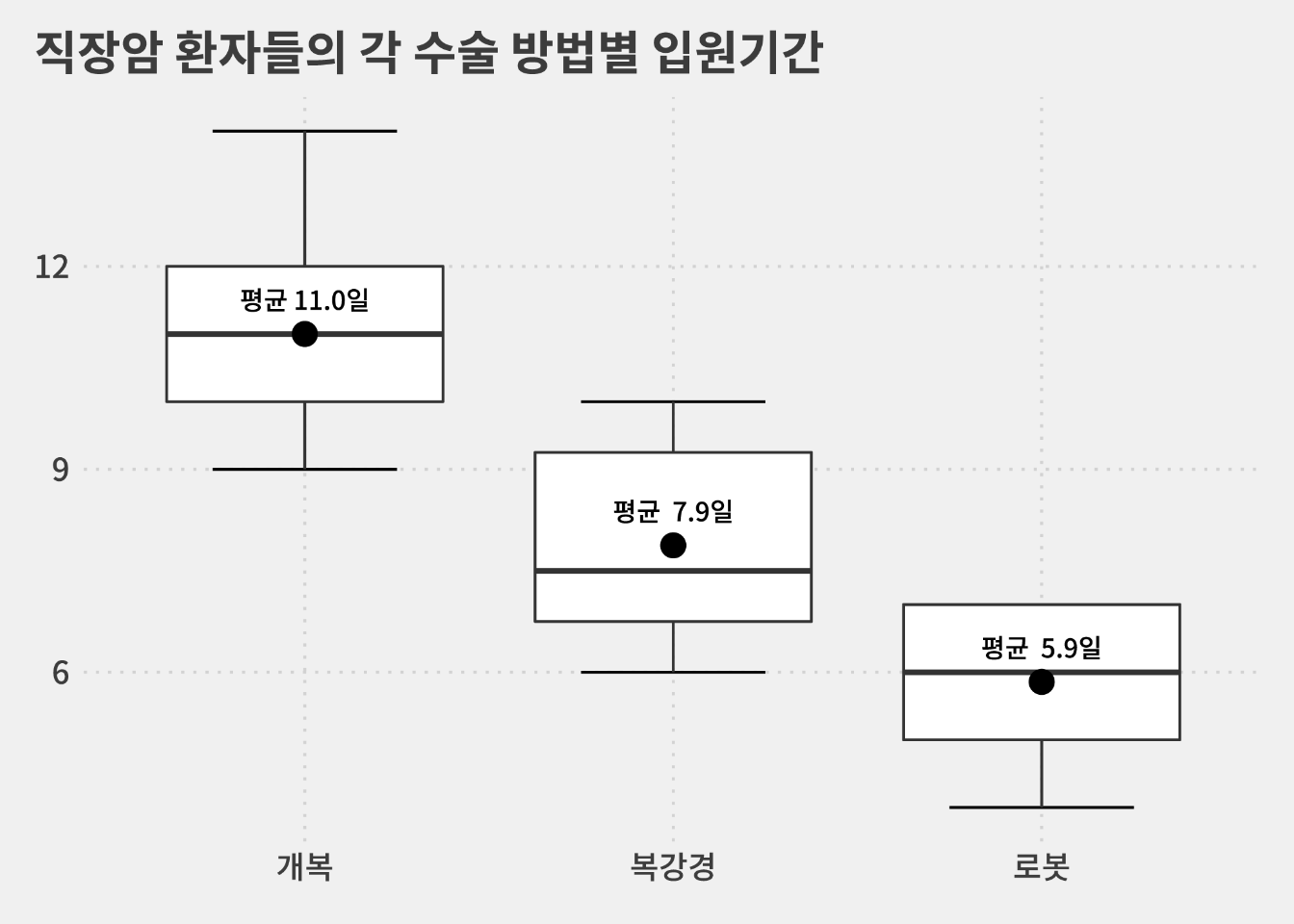
ANOVA는 결국 평균을 비교하는 작업이라 평균이 중요한 겁니다.
위에 있는 그래프에 이미 결과가 나와있지만 수술 방법별 평균을 계산하는 코드는 이렇게 쓸 수 있습니다.
tidyverse 초심자 여러분도 '최대한 친절하게 쓴 R로 데이터 뽑아내기(feat. dplyr)' 포스트를 읽어 보셨다면 이 정도 코드는 어렵지 않게 이해하실 수 있을 겁니다.
enframe(
list(개복 = c(12, 10, 14, 12, 11, 9, 9, 11, 11),
복강경 = c(9, 7, 8, 6, 6, 7, 10, 10),
로봇 = c(5, 6, 7, 7, 7, 4, 5))
) %>%
unnest(value) %>%
group_by(name) %>%
summarise(mean = mean(value))## # A tibble: 3 x 2 ## name mean ## <chr> <dbl> ## 1 개복 11 ## 2 로봇 5.86 ## 3 복강경 7.88
그러면 이 평균값이 정말 유의미하게 차이가 나는지 아닌지 어떻게 알 수 있을까요?
이를 알아보려면 '분산'을 따져봐야 합니다. ANOVA가 '분산 분석'이었던 것 잊지 않고 계시죠?
그럼 분산이 뭔가요? 분산은 편차(deviation)를 제곱한 다음 이를 모두 더해 데이터 개수(n) 나눈 값입니다.
(조금 더 수준을 끌어올리면 표본 분산을 계산할 때는 n이 아니라 n-1로 나누는 게 맞지만 그 내용은 이번 포스트 범위 바깥입니다.)

그러면 편차는 뭘까요? 관측값 그러니까 개별 데이터에서 평균을 뺀 값입니다.
예컨대 우리가 사용하고 있는 자료에서 개복 수술을 받은 첫 환자는 12일 동안 입원했습니다.
개복 수술 평균 입원일은 11일이니까 이때 편차는 1일(= 12일 - 11일)이 됩니다.
그룹 평균 말고 전체 평균과 비교하면 편차를 하나 더 계산할 수 있습니다.
먼저 전체 평균 입원일을 계산하면 8.46일이 나옵니다.
enframe(
list(개복 = c(12, 10, 14, 12, 11, 9, 9, 11, 11),
복강경 = c(9, 7, 8, 6, 6, 7, 10, 10),
로봇 = c(5, 6, 7, 7, 7, 4, 5))
) %>%
unnest(value) %>%
summarise(mean = mean(value))## # A tibble: 1 x 1 ## mean ## <dbl> ## 1 8.46
따라서 이때 편차는 3.54일(= 12일 - 8.46일)이 됩니다.
네, 또 각 그룹과 전체 평균 사이에도 편차를 계산할 수 있습니다.
개복 수술을 받은 환자는 평균 11일 동안 입원을 하니까 이때 편차는 2.54일이 됩니다.
요약하면 △개별 데이터 - 전체 평균 △그룹 평균 - 전체 평균 △개별 데이터 - 그룹 평균 등 세 가지 편차가 존재하는 겁니다.
각 데이터마다 이 세 가지 편차를 계산한 다음 종류별로 더하면 어떤 결과(편차제곱합)가 나올까요?
enframe(
list(개복 = c(12, 10, 14, 12, 11, 9, 9, 11, 11),
복강경 = c(9, 7, 8, 6, 6, 7, 10, 10),
로봇 = c(5, 6, 7, 7, 7, 4, 5))
) %>%
unnest(value) %>%
mutate(편차_제곱 = (value - mean(value))^2) %>%
group_by(name) %>%
mutate(그룹평균 = mean(value)) %>%
ungroup() %>%
mutate(그룹_vs_전체 = (그룹평균 - mean(value))^2,
개별_vs_그룹 = (value - 그룹평균)^2) %>%
summarise(편차_제곱 = sum(편차_제곱),
그룹_vs_전체=sum(그룹_vs_전체),
개별_vs_그룹=sum(개별_vs_그룹))## # A tibble: 1 x 3 ## 편차_제곱 그룹_vs_전체 개별_vs_그룹 ## <dbl> <dbl> <dbl> ## 1 156. 108. 47.7
반올림 때문에 숫자가 딱 떨어지게 나오지는 않았습니다.
소수점 자리를 늘려보면 각 편차제곱합은 △155.9 △108.2 △47.7이 됩니다.
암산에 능한 분이라면 155.9 = 108.2 + 47.7이라고 계산하셨을지 모릅니다.
뭔가 재미있는 일이 벌어지고 있는 것 같지 않습니까?
맨 앞에 나오는 편차제곱합은 전체 분산을 나타냅니다.
그다음 숫자는 그룹 사이에 존재하는 분산(그룹 간 분산)입니다.
마지막 숫자는 그룹 내에서 각 데이터가 얼마나 차이(그룹 내 분산)가 나는지 알려줍니다.
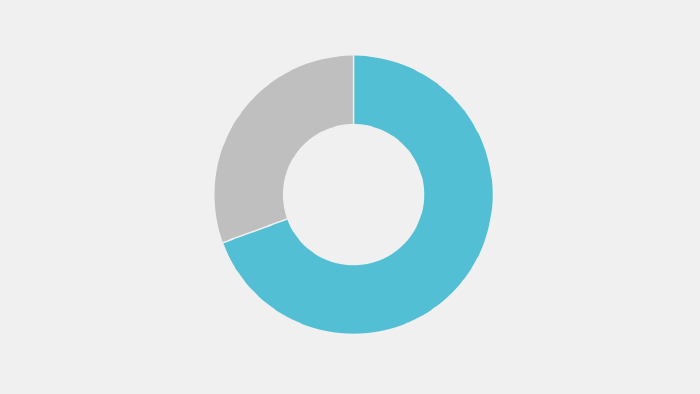
따라서 우리는 전체 분산(155.9) 가운데 108.2(69.4%)를 그룹 간 분산으로 설명할 수 있다고 풀이할 수 있습니다.
108.2 / 155.9## [1] 0.6940346
유심히 보신 분이 드물겠지만 사실 우리는 앞에서 이 숫자를 본 적이 있습니다.
enframe(
list(개복 = c(12, 10, 14, 12, 11, 9, 9, 11, 11),
복강경 = c(9, 7, 8, 6, 6, 7, 10, 10),
로봇 = c(5, 6, 7, 7, 7, 4, 5))
) %>%
unnest(value) %>%
mutate(name = name %>% as_factor()) %>%
summarise(aov(value ~ name, data = .) %>% glance())## # A tibble: 1 x 6 ## logLik AIC BIC deviance nobs r.squared ## <dbl> <dbl> <dbl> <dbl> <int> <dbl> ## 1 -42.3 92.6 97.3 47.7 24 0.694
여기 등장하는 r.squared 그러니까 결정계수 R²이 바로 0.694입니다.
역시나 관례적으로 자연과학이나 공학에서는 0.7, 사회과학에서는 0.3을 R² 문턱값으로 제시합니다.
이 정도 숫자는 넘어야 모형이 쓸모가 있다고 판단하는 겁니다.
다시 말씀드리지만 이는 관례일 뿐 이 문턱값만 가지고 모형 성능을 평가하는 건 곤란합니다.

p-값도 짚고 넘어가야 할 개념입니다.
p-값은 기본적으로 영가설(H0)이 맞다고 가정했을 때 현재 데이터보다 '극단적인' 데이터를 관측할 수 있는 확률을 나타냅니다.
영가설 또는 귀무가설은 문자 그대로 아무 것 그러니까 아무 차이도 없는 상황을 가정합니다.
따라서 이번 자료에서 영가설은 '수술 방법별 입원일수에는 차이는 없다'가 됩니다.
앞에서 했던 것처럼 다시 tidy() 함수로 확인해보면 p-값은 0.00000399입니다.
enframe(
list(개복 = c(12, 10, 14, 12, 11, 9, 9, 11, 11),
복강경 = c(9, 7, 8, 6, 6, 7, 10, 10),
로봇 = c(5, 6, 7, 7, 7, 4, 5))
) %>%
unnest(value) %>%
mutate(name = name %>% as_factor()) %>%
summarise(aov(value ~ name, data = .) %>% tidy())## # A tibble: 2 x 6 ## term df sumsq meansq statistic p.value ## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 name 2 108. 54.1 23.8 0.00000399 ## 2 Residuals 21 47.7 2.27 NA NA
따라서 실제로는 수술 방법별 입원일수에 차이가 없는데 이런 결과가 나올 확률은 0.000399%밖에 되지 않습니다.
ANOVA을 진행할 때 주의해야 할 건 연구가설 또는 대립가설은 '그룹별로 차이가 난다'가 아니라 '적어도 하나는 차이가 난다'라는 점입니다.
그러니까 만약 복강경, 로봇 수술 사이에는 입원일수 차이가 없고 개복 수술만 차이가 난다고 하더라도 p-값이 낮게 나올 수 있는 겁니다.
또 이 p-값을 의도적으로 낮추는 방법이 차고 넘쳐난다는 점도 잊어서는 안 됩니다. (이를 흔히 'p-해킹'이라고 부릅니다.)
그래서 다시 한 번 강조하건대 p-값이 어떤 값 이상 또는 이하라는 이유만으로 결론을 내리는 건 올바르지 못한 접근법입니다.
그러면 p-값은 어떻게 계산할까요?
이때 필요한 숫자가 바로 statistic(통계량)입니다.
ANOVA에서 통계량은 F값이고 마지막 분석 결과를 통해 이 자료에서는 23.8이라는 사실을 알 수 있습니다.
이 값을 그래프에 표시하면 아래처럼 나타납니다.
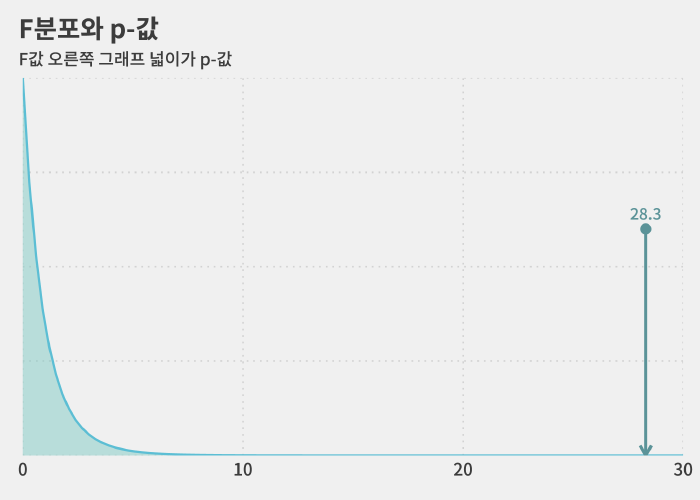
특정한 F값이 있을 때 그 값보다 오른쪽에 있는 그래프 넓이가 바로 p-값이 됩니다.
F분포에 대한 개념이 없으시다면 이 문장이 무슨 뜻인지 도대체 모르겠다고 생각하시는 게 당연한 일입니다.
도대체 이게 무슨 소리인지 궁금해 죽겠다는 분이 계시다면 졸고(卒稿) '친절한 R with 스포츠 데이터'를 추천해 드립니다.
모쪼록 이 책이 R로 데이터 과학을 공부해 보고 싶은 분이 기본기를 쌓는 데 도움이 됐으면 좋겠습니다.
그럼 모두들 Happy Tidyversing -_-)/
데이터 과학 입문서 '친절한 R with 스포츠 데이터'를 썼습니다
어쩌다 보니 '한국어 사용자에게 도움이 될지도 모르는 R 언어 기초 회화 교재'를 세상에 내놓게 됐습니다. 책 앞 부분은 '한국어 tidyverse 사투리' 번역, 뒷부분은 'tidymodels 억양 따라하기'에 초점
kuduz.tistory.com
댓글,